A Comprehensive Guide to Computing Manhattan Distance in Python

1. Basis of Manhattan Distance

Manhattan Distance is a distance metric that measures the distance between two points in a grid-like system. It is also known as the city block distance or taxi cab distance. The Manhattan distance between two points (x1, y1) and (x2, y2) in a two-dimensional space is calculated as the sum of the absolute differences between their x-coordinates and y-coordinates:

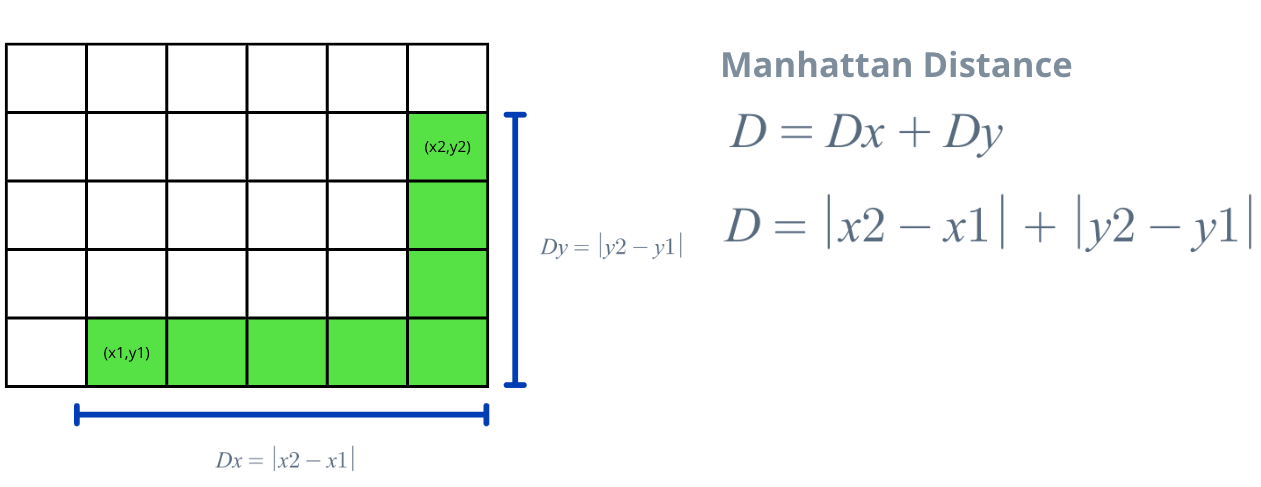
understanding-manhattan-distance

$\text{Manhattan Distance} = |x_2 - x_1| + |y_2 - y_1|$

2. Python Implementation

2.1. Required Libraries

In order to compute Manhattan Distance in Python, you will need to use the NumPy library. NumPy is a Python library used for working with arrays.

To install NumPy, you can use pip, which is a package manager for Python. Here are the steps to install NumPy:

Open a command prompt or terminal.
Type pip install numpy and press Enter.
Wait for the installation to complete.

2.2. Setting up the Environment

To create a Python environment for your project, you can use either Jupyter Notebook or Google Colab. Both are popular tools for creating and organizing computation documents.

3. Practical Example

3.1. Real-World Use Cases

The Manhattan distance is a popular distance metric used in many fields, including data science, gaming, and computer vision. Here are some examples of where the Manhattan distance is applied:

Data Science: The Manhattan distance is used in clustering algorithms such as K-Means and K-Nearest Neighbors (KNN) to measure the distance between data points.
Gaming: The Manhattan distance is used in pathfinding algorithms such as A* to find the shortest path between two points on a grid.
Computer Vision: The Manhattan distance is used in image processing and computer vision to measure the similarity between two images.

3.2. Python Code for Examples

Here is the Python code for computing the Manhattan distance between two points in a two-dimensional space:

import numpy as np

def manhattan_distance(x1, y1, x2, y2):
    return np.abs(x2 - x1) + np.abs(y2 - y1)

print(manhattan_distance(1, 2, 3, 4)) # 4
print(manhattan_distance(1, 2, 3, 2)) # 2
print(manhattan_distance(1, 2, 1, 2)) # 0

This code defines a function manhattan_distance that takes two NumPy arrays as input and returns their Manhattan distance. You can use this function to calculate the distance between any two points in a grid-like system.

4. Conclusion

In this article, you learned how to compute the Manhattan distance between two points in a two-dimensional space using Python. You also learned about the applications of the Manhattan distance in data science, gaming, and computer vision.