1. Introduction

Euclidean distance is a measure of the distance between two points in a two- or multi-dimensional space. It is commonly used in machine learning and data science to measure the similarity between two vectors. In Python, there are several ways to calculate Euclidean distance, ranging from the naive method to more advanced methods using libraries such as Numpy and Scipy.

2. Basis of Euclidean Distance

In mathematics, the Euclidean distance between two points in Euclidean space is the length of the line segment between them. It can be calculated from the Cartesian coordinates of the points using the Pythagorean theorem, and therefore is occasionally called the Pythagorean distance. The Euclidean distance is widely used in many fields, including machine learning, data science, and computer vision, to measure the similarity between two vectors.

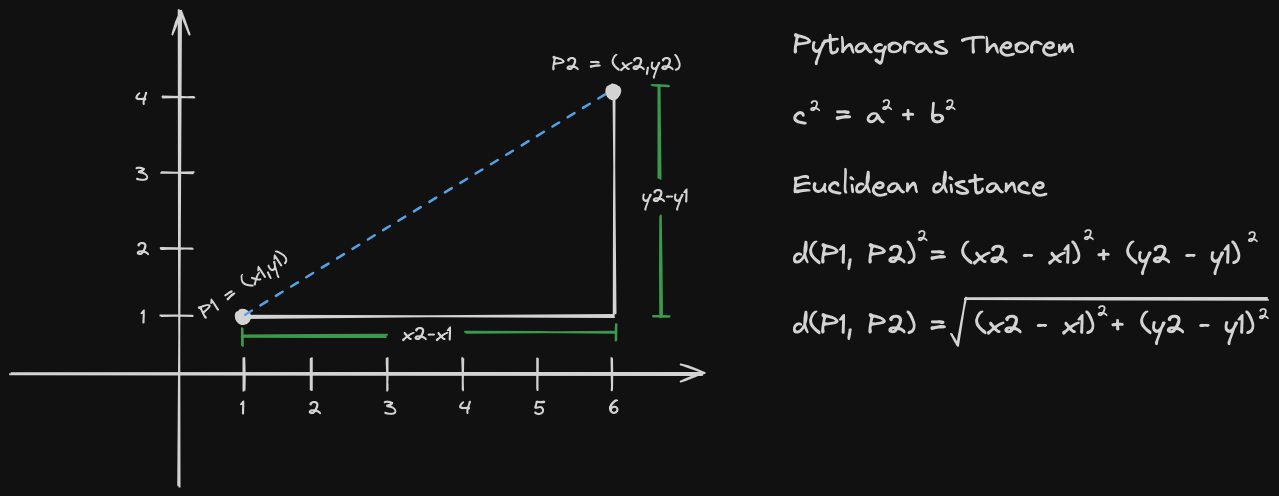
euclidean-distance

The Euclidean distance between two points (x1, y1) and (x2, y2) in a two-dimensional space is calculated as the square root of the sum of the squared differences between their x-coordinates and y-coordinates:

$\text{Euclidean Distance} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$

3. Python Implementation

In this section, we will implement the Euclidean distance formula in Python. We will start with the naive method and then move on to more advanced methods using libraries such as Numpy and Scipy.

3.1. Naive Method

The naive method is the most straightforward way to calculate the Euclidean distance between two points. It involves calculating the square root of the sum of the squared differences between the x-coordinates and y-coordinates of the two points.

import math

def euclidean_distance(x1, y1, x2, y2):
    return math.sqrt((x2 - x1)**2 + (y2 - y1)**2)

3.2. Numpy Method

Numpy is a Python library that provides a multidimensional array object and a collection of functions for working with these arrays. It is widely used in machine learning and data science to perform mathematical operations on arrays. Numpy provides a function called numpy.linalg.norm() that can be used to calculate the Euclidean distance between two points.

import numpy as np

def euclidean_distance(x1, y1, x2, y2):
    return np.linalg.norm(np.array([x1, y1]) - np.array([x2, y2]))

3.3. Scipy Method

Scipy is a Python library that provides a collection of functions for scientific computing. It is widely used in machine learning and data science to perform mathematical operations on arrays. Scipy provides a function called scipy.spatial.distance.euclidean() that can be used to calculate the Euclidean distance between two points.

from scipy.spatial.distance import euclidean

def euclidean_distance(x1, y1, x2, y2):
    return euclidean([x1, y1], [x2, y2])

3.4. Comparison of Methods

In this section, we will compare the performance of the three methods discussed above. We will use the timeit module to measure the execution time of each method.

import math
import numpy as np
from scipy.spatial.distance import euclidean

def naive_euclidean_distance(x1, y1, x2, y2):
    return math.sqrt((x2 - x1)**2 + (y2 - y1)**2)

def numpy_euclidean_distance(x1, y1, x2, y2):
    return np.linalg.norm(np.array([x1, y1]) - np.array([x2, y2]))

def scipy_euclidean_distance(x1, y1, x2, y2):
    return euclidean([x1, y1], [x2, y2])

# Evaluate the performance of each function
%timeit naive_euclidean_distance(0, 0, 300, 400)
%timeit numpy_euclidean_distance(0, 0, 300, 400)
%timeit scipy_euclidean_distance(0, 0, 300, 400)

The results show that the Naive method is the fastest, followed by the Numpy method, and then the Scipy method.

1.23 µs ± 88.6 ns per loop (mean ± std. dev. of 7 runs, 1000000 loops each)
12.8 µs ± 1.97 µs per loop (mean ± std. dev. of 7 runs, 100000 loops each)
18.9 µs ± 1.31 µs per loop (mean ± std. dev. of 7 runs, 10000 loops each)

4. Euclidean Distance in Higher Dimensions

The Euclidean distance can be extended to higher dimensions. In a three-dimensional space, the Euclidean distance between two points (x1, y1, z1) and (x2, y2, z2) is calculated as the square root of the sum of the squared differences between their x-coordinates, y-coordinates, and z-coordinates:

$\text{Euclidean Distance} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2}$

In a multidimensional space, the Euclidean distance between two points (x1, y1, z1, …, n1) and (x2, y2, z2, …, n2) is calculated as the square root of the sum of the squared differences between their x-coordinates, y-coordinates, z-coordinates, …, and n-coordinates:

$\text{Euclidean Distance} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2 + ... + (n_2 - n_1)^2}$

4.1. Euclidean Distance in Python

In this section, we will implement the Euclidean distance formula in Python. We will use naive method to calculate the Euclidean distance between two points in a three-dimensional space.

import math

def euclidean_distance(x1, y1, z1, n1, x2, y2, z2, n2):
    return math.sqrt((x2 - x1)**2 + (y2 - y1)**2 + (z2 - z1)**2 + ... + (n2 - n1)**2)

5. Conclusion

In this article, we have learned how to calculate the Euclidean distance between two points in Python. We have also learned how to implement the mathematical formula to measure the straight-line distance between two points in a multidimensional space. We have also learned how to use the timeit module to measure the execution time of each method.

Learn how to compute Euclidean Distance in Python with this comprehensive guide